计算理论：正则表达式

course notes › theory of computation

Regular expression

Definition of RE

Regular expressions describe language (regular languages)

If is a regular expression, is the language it defines

RE 的定义是递归的。RE 使用三种语言上的基本操作：Union, Concatenation, Kleene Star

  • Union:
  • Concatenation:
  • Kleene Star:

根据以上操作，即可给出 RE 的递归定义，RE 是 expression，由操作符和操作符连接起来的表达式构成，在给出 RE 的同时也将给出 RE 定义的语言

Basis.

  • Basis 1: If is any symbol, then is a RE,
  • Basis 2: is a RE,
  • Basis 3: is a RE,

Induction.

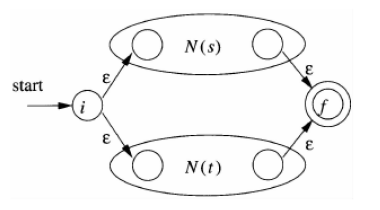
  • Induction 1: If are RE, is a RE,
  • Induction 2: If are RE, is a RE,
  • Induction 3: If is a RE, then is a RE,
  • Induction 4: if is a RE, then is a RE,

操作优先级由高到低是 ，concatenation，

Algebraic Laws for RE:

  • Union is commutative and associative, concatenation is associative
  • Concatenation distributes over union
  • is the identity for +,
  • is the identity for concatenation,
  • is the annihilator for concatenation,
  • Union is idempotent:

Laws Involving Closures:

如何判断一个 RE 的代数定律是否为真：代入一个具体的 RE （见书 3.4.7 节）

Equivalence of RE and FA

RE to FA

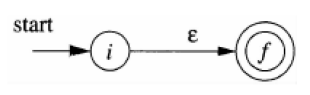
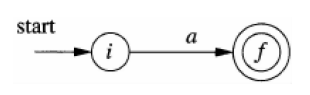
For every RE, there is a FA that accepts the same language

Pick -NFA

Basis.

Induction. 假设正则表达式 的 NFA 为

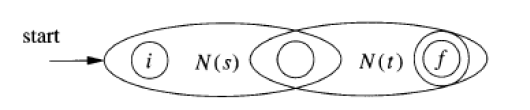
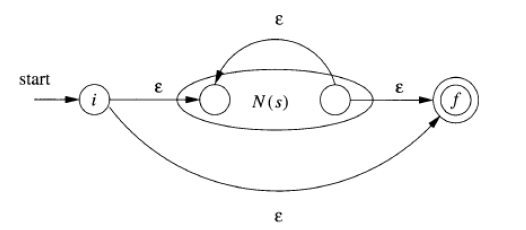
FA to RE

For every FA, there is a RE defining its language

Pick DFA

使用归纳。假设 DFA 的状态为

定义 -Path: A -Path is a path through the graph of the DFA that goes through no state numbered higher than

-path 的 endpoint 没有限制，-path 可以是任意路径

则该 DFA 对应的 RE 是所有从开始状态到接受状态的 -path 的 RE 的集合

Proof.

其正确性的证明基于对 的归纳，令 为从状态 到状态 的 -path 上的 label 表示的 RE

Basis. ，此时 是从 到 所有边上的标号的和

  • 若没有边，则为
  • 若 ，则需要加上

Induction. 从 到 的 -path，或者经过状态 （一次或多次），或者不经过状态

  • 经过状态 ：
  • 不经过状态 ：

故

Q.E.D.

The RE with the same language as the DFA is the union of where

  • is the number of states
  • is the start state
  • is one of the final states

Properties of Regular Languages

Properties

A language class is a set of languages

Language classes have two important kinds of properties

  • Decision properties （判定性）
  • Closure properties （封闭性）

Closure properties: given languages in the class, an operation produces another language in the same class

Decision properties: an algorithm that takes a formal description of a language and tells whether or not some property holds

  • Membership problem: is string in regular language
  • Emptiness problem: does the language contain any string at all

Pumping Lemma

Let be a regular language. Then there exists a constant (which depends on ) such that for every string in such that , we can break into three strings, , such that:

  3. For all , the string is also in

pumping lemma 可以用于证明一个 language 不是 RL

Decision Properties of Regular Language

The membership problem: Given a string and a regular language , is in

Algorithm: Simulate the DFA, if the DFA ends in an accepting state, the answer is "yes", otherwise the answer is "no"

The emptiness problem: Given a regular language, does the language contain any string at all

Algorithm: Compute the set of states reachable from the start state. If at least one final state is reachable, then yes, else no.

reachable 的定义是递归给出的

Basis. The start state is surely reachable from the start state.

Induction. If state is reachable from the start state, and there is an arc from to with any label (input or ), then is reachable

如果语言由 RE 给出，则可根据以下递归规则判断是否为空

Basis. denotes the empty language, and for any input symbol do not.

Induction. Suppose is a RE. There are four cases to consider.

  1. . Then is empty is empty and is empty
  2. . Then is empty is empty or is empty
  3. . Then is not empty, it always includes at least
  4. . Then is empty is empty

The infiniteness problem: Is a given language infinite?

Key Idea: if the DFA has states, and the language contains ant string of length or more, then the language is infinite.

Suppose that is a regular language accepted by a DFA with states. Then is infinite contains a word whose length is at least .

Proof.

: 如果一个有 个状态的 DFA 接受一个长度至少为 的字符串 ，则在其路径上至少有一个状态出现两次（PHP）。设其路径为

设从 到第一个 的标号组成串 ，从第一个 到第二个 的标号组成串 ，从第二个 到 组成字符串 ，则该 DFA 可接受所有形如 的字符串 (i. e. pumping lemma)

: trivial

Q.E.D.

However, there are an infinite number of strings of length , and we can't test them all

Key Idea: if there is a string of length in , then there is a string of length between and

Suppose that is a regular language accepted by a DFA with states. Then is infinite contains a word whose length is between and .

Proof.

: 因为 是 infinite，其包含一个 string 长度至少为 ，设 为 包含的长度至少为 的 string 中最短的

设 DFA 接受其的状态顺序为 ，根据 PHP ，其中必有一个状态至少出现两次，设其为 ，且 ，故 也属于 。根据 的定义，有 ，又 且 ，故 。根据其定义 ，故可得

: 同上（pumping lemma）

Q.E.D.

根据以上两个 key idea，检查所有长度在 到 之间的串即可

然而在实际中这样的算法代价也是不可接受的。所以一般是通过检查 DFA 对应的图中是否有环来判断语言是否 infinite。具体而言分为以下几步

  1. Eliminate states not reachable from the start state
  2. Eliminate states that do not reach a final state
  3. Test if the remaining transition graph has any cycles

The equivalence problem: Given regular languages and , is

Algorithm: Constructing the product DFA from DFA for

设 与 的 DFA 有状态集合 与 ，则 product DFA 有状态集合

对于 product DFA 而言

  • start state:
  • transition:
  • final states: states that exactly one of and is a final state of its own DFA

由于 product DFA 的 accept state 是两个状态中有且仅有一个是原本的 accept state，则如果一个 string 被 product DFA 接受，说明其被一个 DFA 接受而不被另一个 DFA 接受

the product DFA's language is empty

The containment problem: Given regular languages and , is

Algorithm: use the product DFA

final state: states that is the final state, is not

the product DFA's language is empty

The Minimum-State DFA for a Regular Language

Equivalence of states

Given a DFA , find the DFA with the fewest states accepting (equivalence)

Equivalence of states: states and are equivalent if

For all input strings , is an accepting state is an accepting state

If two states are not equivalent, then we say they are distinguishable. That is, state is distinguishable from state if there is at least one string such that one of and is accepting, and the other is not accepting.

Algorithm: table-filling algorithm

  • Construct a table with all pairs of states
  • If you find a string that distinguishes two states (takes exactly one to an accepting state), mark that pair
  • Algorithm is a recursion on the length of the shortest distinguishing string
    • Basis. If is an accepting state and is non-accepting, then the pair is distinguishable
    • Induction. Let and be states such that for some input symbol , and are a pair of states known to be distinguishable. Then is a pair of distinguishable states.

在算法结束后，所有未被标记的 pair 是等价的状态

If two states are not distinguished by the table-filling algorithm, then the states are equivalent.

Proof.

假设命题错误，故存在至少一对状态 满足

  • is distinguishable.
  • the algorithm does not find and to be distinguishable

令这样的状态对为 bad pair。则对于所有 bad pairs，都存在一个 string 来区分两个状态。令其中 string 最短的 pair 为 ，区分其的最短 string 为

显然 ，否则在 Basis 阶段就被区分，即 。考虑 ，显然， 区分 ，但是 比任何能区分 bad pair 的 string 都短，故 不是 bad pair，算法将其标记为 distinguishable。于是根据 Induction 的部分，算法发现 是 distinguishable，因为 是 distinguishable。矛盾。故原命题正确

Q.E.D.

对于 Equivalence problem，也可以通过这个算法解决。若判断两个 regular languages 是否等价，可以将其状态合并，即 ，然后对其应用 table-filling algorithm

两个 DFA 的开始状态 等价

Minimize DFA

要最小化一个 DFA ，首先要合并所有不可区分的状态

状态的合并可按照如下步骤

  • 假设 是不可区分的
  • 将其用一个代表状态 代替
  • 显然 也是不可区分的（否则其中必有至少一对被算法标记为 distinguishable）
  • 令 为 的代表元素

合并之后，还要去掉所有从开始状态不可达的状态

事实上，状态的等价是一种等价关系，所以所有等价的状态将状态集划分为多个不相交的等价类

The equivalence of states is transitive

Proof.

假设 与 是等价的，但 不等价。根据定义，存在一个输入 string 满足 与 中有且仅有一个是接收状态

w.l.o.g. 是接收状态。考虑 ，若其为接收状态， 为 distinguishable，若其为非接受状态， 为 distinguishable。均与假设矛盾

Q.E.D.

故最小化 DFA 即为

  • 消去所有从开始不可达的状态
  • 将状态根据等价关系（由 table-filling algorithm 得到）划分为等价类
  • 将含有不止一个状态的等价类合并为一个代表状态
  • 合并状态转移

包含开始状态的等价类为新 DFA 的开始状态，包含接受状态的等价类为新 DFA 的接收状态

Minimized DFA can't be beaten

If is a DFA, and the DFA constructed from by the algorithm of minimizing DFA, then has as few states as any DFA equivalent to

事实上，对于一个 DFA ，其所有最小的 DFA 都是同构的

Proof.

假设 是一个 DFA，最小化其得到 DFA ，假设存在一个 DFA 与 接受一样的 language，但有更少的状态。考虑 组合的 DFA，首先

  • 的开始状态是等价的，因为
  • 若状态 等价，则 等价

对于每个 中的状态 ， 其与 中至少一个状态等价：

Proof.

Basis. 如果 是 的开始状态，其与 的开始状态等价

假设从 的开始状态到达 的最短路径长度为

I.H. 若从 的开始状态到达 的最短路径长度短于 ，则存在一个 中的状态与其等价

Induction. 假设从 的开始状态到 的最短路径的 string 为 ，长为 。假设从 开始状态出发沿 到达 ，从 开始状态出发沿 到达 ，根据 I. H. ， 等价。故 等价

Q.E.D.

由于根据前提， 状态数少于 ，故至少有两个 中的状态与 中的同一个状态等价。因此这两个状态等价，这与 中所有状态都不等价矛盾，故前提错误，不存在这样的

Q.E.D.

Closure Properties of Regular Language

Closure Under Union: If and are regular languages, then so is

Proof.

如果 为正则语言，则其有对应的 RE ，即 ，根据 RE 的定义，有 ，显然 为正则语言

Q.E.D.

Concatenation 与 Kleene Closure 的证明同理，根据 RE 的定义即可证明其封闭性： 是 的 RE， 是 的 RE

Closure Under Complementation: If is a regular language over alphabet , then is also a regular language

Proof.

Let for some DFA , then , where is the DFA

即构造一个 DFA 使得其所有接收状态都为 中的非接受状态，这样对于任意字符串 都有

于是得到

即 是由 DFA 定义的正则语言

Q.E.D.

Closure Under Intersection: If and are regular languages, then so is

Proof.

可以通过 De Morgan‘s Law 以及 Complementation 和 Union 的封闭性证明

也可通过直接构造 DFA 证明。设 对应的 DFA 为 ，则构造 product DFA ，其中

这样对于任意字符串 有

则有

Q.E.D.

已知 不是 RE

为有相等个 0 和 1 的串的集合，则 不是 RE

Proof.

若 是 RE，则 为 RE，矛盾，故 不是 RE

Q.E.D.

Closure Under Difference: If and are regular languages, then so is

Proof.

，根据 complementation 与 intersection 的封闭性， 也是 RE

Q.E.D.

Closure Under Reversal: 对于一个字符串 ，其 reversal ，对于一个语言 , If is a regular language, so is

Proof.

Automaton-based proof

对于 的 DFA

  1. 将 的转换图中的边反转
  2. 令 的开始状态为唯一的接收状态
  3. 添加一个开始状态 ，以及从 到其他接收状态的 -transition

则

RE-based proof

假设 的 RE 为 ，存在一个 RE 使得 。对 的长度归纳

Basis.

Induction.

  • , then
  • , then
  • , then

Q.E.D.

Closure Under Homomorphisms: A string homomorphism is a function on strings that works by substituting a particular string for each symbol

If is a homomorphism on alphabet , and is a string of symbols in ,then

For language

If is a regular language over alphabet , and is a homomorphism on , then is also regular.

Proof.

令 为 的 RE，对 应用 得到 ，则 定义语言 ，证明为对 的子表达式 归纳证明

Basis.

如果 是 或 ，则 ，因为 不影响 或 。显然， 。又因为 为 或 ，则 ，故

如果 是 ， ，根据定义， ，同理， 是符号 组成的 string，则 ，故

Induction.

Union: 根据定义，有 ，根据 + 的定义

以及

又因为 独立地应用于语言中的每个字符串，有

根据 I. H. ，故

Concatenation 与 Kleene star 的证明类似

可以证明将 应用于一个语言 的 RE 可以得到一个定义了语言 的 RE

Q.E.D.

Closure Under Inverse Homomorphisms: Suppose is a homomorphism from alphabet to strings in another (possibly the same) alphabet . Let be a language over alphabet . Then

If is a homomorphism from alphabet to alphabet , and is a regular language of , then is also a regular language

Proof.

令 ，其中 。定义 DFA

其中转换函数定义为

对于输入 的转换的结果是 对于输入串 的转换结果。根据字符串 的长度归纳，可以轻松地得出 ，由于 的接收状态相同，故

从而有

Q.E.D.