计算理论：可判定性与复杂度

course notes › theory of computation

Decidability and Complexity

Decidability

Diagonalization method

Diagonalization method 是康托尔提出的一种数学证明方法，用于证明某个集合是不可数的（即无法建立起该集合和自然数集之间的双射）

Uncountable sets

自然数集 是 countable 的

一个集合 是 countable，满足其是有限集，或其是无限集且存在一个 bijection

E.g. 有理数集是 countable 的，但是实数集是 uncountable 的

Proof.

如果实数集是 countable，则存在一个双射 ，使得每一个实数都有一个唯一的整数 对应，则将所有实数按照自然数的顺序排列，则令

其中 不等于 小数点后的第 位数字。显然 是一个实数，且如果存在满足要求的双射，则 也有一个对应的自然数 ，则产生矛盾，如果 是第 个实数，则其小数点后第 位应当等于 小数点后第 位，而这与 的定义矛盾，故实数集是 uncountable

Q.E.D.

Non-RE languages

根据之前的结论，语言之间的包含关系为

regular language CFL recursive language RE all language

前两个真包含关系已经可以根据形如 的语言得出，现在首先证明最后一个真包含关系，即：存在语言不是 RE language

证明分为三步

  • 证明所有 TM 的集合是 countable 的
  • 证明所有 language 的集合是 uncountable 的
  • 根据上述结论，不可能存在从 TM 集合到 language 集合的满射

1). 所有 TM 的集合是 countable 的

Proof.

所有 string 的集合 是 countable 的，因为可以将所有 string 按照其长度和字典序排成一列，为其标号

而每个图灵机 可以表示为一个有限长度的 string，设其为 ，则从所有 string 的集合中删去所有不是 TM 的 string，则得到 TM 的集合，显然这个集合是 countable 的

Q.E.D.

2). 所有 language 的集合是 uncountable 的

Proof.

所有 string 的集合是 countable 的，则可以将每个 string 编号，得到 ，则一个 language 可以由一个特征向量 描述，如果 则 ，否则 ，则同样使用对角法，假设所有 language 的集合是 countable，则对每个特征向量存在一个唯一的自然数与其对应。则考虑语言

即如果第 个语言包含 则 不含 ，反之亦然

则如果所有 language 的集合是 countable 则产生矛盾，若 对应的自然数为 ，则按照映射如果 则 ，按照定义则 ，即 ，矛盾

Q.E.D.

由于 TM 的集合是 countable 而 language 的集合是 uncountable，故存在语言不会被任何 TM 接受

The halting problem is undecidable

Halting problem

停机问题的定义是语言

其中 是 TM 和 的字符串形式

显然这个语言是 RE，模拟 对于 为输入的运行即可，现在需要证明 HALT 是否是 decidable，即是否存在一个 algorithm 接受 HALT。结论是 HALT 不是 decidable 的

Proof.

以下给出大致的证明流程

假设存在 TM decides HALT，即如果 在 上 halt， 接受，否则 拒绝

则定义一个新的 TM ，对于输入 ，如果 接受 ，则无限循环，否则 halt

现在考虑将 输入 ，则如果 halt，按照定义说明 拒绝 ，而按照 的定义， 不应当 halt，反之亦然，矛盾

根据反证法， 均不存在

Q.E.D.

使用对角法也可以证明该结论，思路与上文类似

RE and co-RE

一个 RE 的补叫做 co-RE，而所有 co-RE 的集合组成了 co-RE 语言（注意 co-RE 不是非 RE）

则有结论：一个语言 是 decidable 是 RE 且 是 co-RE

Proof.

显然 如果是 decidable 则 一定是 RE，则 的补只需要反转 TM 的接受/拒绝，则 的补同样是 RE，得出 是 co-RE

易得存在 TM 接受 L，以及存在 TM 接受 的补，则只需要构造 TM 平行模拟 ，当 接受则接受，当 接受则拒绝，即得到一个 algorithm 接受 ， 为 decidable

Q.E.D.

根据上述结论，可以得出 HALT 的补不是 RE。如果 HALT 的补是 RE，则 HALT 是 co-RE，根据上文结论，HALT 为 decidable，而这与之前的结论相矛盾

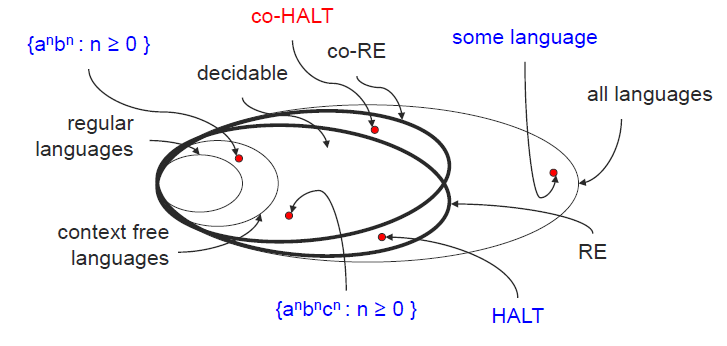
2019-11-24_19-26-40.png

上述图片阐明了各个语言之间的关系

Undecidable Problems about TM

Reductions

归约（reduction）是一种转换。如果存在一个转换将问题 的实例转换为问题 的实例，且输出相同（如果该实例在 中是 YES，则转换后的实例在 中也是 YES），则称 reduces to ，一般记为

归约可以说明 至少和 一样难，因为如果存在一个可以解决 的 oracle，可以通过归约解决 ，但反之不成立

归约不要求一定是满射和单射，事实上一般 映射过去后的集合只是 的一个子集。

更为正式的定义如下：

Many-one reduction: 考虑 是 alphabet 上的形式语言，则从 到 的一个 Many-one reduction 是一个 可计算的函数 满足

Computable: is computable if there exists a TM s. t. on every , halts on with written on its tape

若存在满足的 则称 m-reduces to ，记为

如果 是 injective 则称 1-reduces to ，记为

如果存在一个 到 的 reduction，则有

  • 如果 undecidable，则 undecidable
  • 如果 是 non-RE，则 是 non-RE

Proof.

考虑陈述 1，如果 是 undecidable，但 是 decidable，则可以通过 reduction 将 的实例 转换为 ，然后使用 的 decider 判定 ，从而 也可判定，矛盾

陈述 2 同理，可以通过 的 recognizer 和 reduction 构造 的 recognizer，导出矛盾

Q.E.D.

因此 reduction 可以用来证明语言的 undecidable/non-RE

假设已知 是已知的 undecidable 的语言，欲证 是 undecidable，步骤为

  • 假设 是 decidable，则存在 decider
  • 使用 判定 （即构造从 到 的 reduction ，对于任意 ，使用 判定 ）
  • 这样得出 是 decidable，导出矛盾，根据归谬法， 是 undecidable

is undecidable

的定义为

而根据上文结论，已知 HALT 是 undecidable 的，那么通过 reduction 可以证明 是 undecidable

Proof.

将 HALT 归约到

如果 可判定，可以通过 判定 HALT，从而导出矛盾

对于 HALT 的实例 ，可以构造一个 TM ，对于输入 判断 是否属于

  • 如果属于，则说明 halt 并接收 ， accept
  • 如果不属于，则说明 或是 halt 并 reject ，或是在 上无限循环
    • 构造 ，模拟 的运行，且当 halt 时，若 结果为 accept 则 reject，反之若 结果为 reject 则 accept，若 无限循环则 同样会无限循环
    • 判断 是否属于 ，如果属于则说明 在 上 halt 并 reject，则 accept，否则说明无论 在 上都循环， reject

由于 可判定，故 最终总会 halt，且有 ，而 HALT 为 undecidable，矛盾。

Q.E.D.

除了归约的证明，也可以直接用归谬法证明

Proof.

如果 decidable，假设其 decider 为 ，则构造 TM 接受 输入

  • 如果 则 reject
  • 如果 则 accept

则考虑 以 为输入，如果 accept，说明 ，即 ，导出矛盾。反之亦然，故根据归谬法，不存在 和 ，亦即 为 undecidable

Q.E.D.

is undecidable

的定义为

是 undecidable 的

Proof.

将 归约到

对于 的实例 ，可以构造一个 TM ， 模拟 在 为输入时的运行

  • 如果 accept ，则 accept 其输入
  • 否则 reject 其输入

如此构造后

如果 decidable 则 也 decidable，导出矛盾，故 undecidable

Q.E.D.

事实上 是 non-RE 的，因为其补是 RE（构造 NTM 猜测一个输入 判断其是否属于 ，只要 非空则一定能猜到一个 并接受 ），而如果 也是 RE 则 为 decidable

Rice's Theorem

Rice's Theorem: all non-trivial, semantic properties of programs are undecidable

semantic property: Rice's theorem 适用范围是关于语言的属性而非关于机器/程序的属性。E.g. 一个程序是否会在所有输入上 halt 就是一个 semantic property，而程序是否会运行超过 1000 步或 TM 是否有超过 5 个状态就不是 semantic property

如果将 property 看作一个接受 TM 为输入的 language ，则如果 ，有

non-trivial: 一个 trivial 的 property 满足：或是所有语言都有该 property ，或是没有语言有该 property。否则其为 non-trivial

is non-trivial if

要注意 Rice's Theorem 的适用范围仅限 non-trivial semantic properties

is non-trivial is undecidable

Proof.

将 归约到

思路为如果 non-trivial 则一定存在 ，对于 的实例 ，构造 TM ，模拟 在 上的运行，如果 accept，则模拟 在输入 上的运行，如果 accept 则 accept，这样

如果 trivial 则证明过程可以推出矛盾，e.g. 包含所有 TM，则

Q.E.D.

以下 properties 都是 undecidable 的

  • 一个 language 是否为空
  • 一个 language 是否有限
  • 一个 language 是否是 regular language
  • 一个 language 是否是 CFL

Complexity

Intractable Problems: problems that cannot to be solvable in polynomial time

Time Complexity

在现实问题中，时间和空间的资源都是有限的，因此需要分析一个 algorithm 所需求的资源

在分析时一般进行 worst-case analysis，一个算法需要的资源是 input string 的长度的函数，而其值是对所有给定长度的 input，算法需要的最大资源数

一个 TM 的 time complexity 是一个函数 ， 是 对于任意长度为 的 input string，所需要运行的最多的步数

在考虑 time complexity 时，通常不考虑精确的步数，且只考虑在输入规模很大的情况下的复杂度。具体而言，使用 asymptotic notation (big-Oh notation)，只关注 的最高项且忽略其常系数

对于函数 ，如果存在正整数 满足对任意

则称

具体含义是规模较大的时候 的增长不会超过

根据 time complexity 即可定义 time complexity class

这里的 TM 指的是 single-tape TM，而对于 multi-tape TM 来说，对于任意 ，任何 的 multi-tape TM 都有一个等价的 的 single-tape TM

是所有能在确定性单带 TM 上以多项式时间判定的语言的集合

是所有能在非确定性单带 TM 上以多项式时间判定的语言的集合

如果定义

则可以定义

对于 中的语言来说，有一个很重要的性质

其中

Proof.

可以构造一个 NTM 判定 ，首先用 步去猜测一个 ，然后用 判定

假设 被一个 的 NTM 判定，则定义 是所有满足“ 是 接受 的一个 accepting computation history” 的 ，则如果 accept ，一定存在一个满足条件的 ，且 （因为 是一个 的 NTM），且

Q.E.D.

被称为 certificate，即对于一个 问题来说，验证其解是一个 问题。

E.g. 最大团问题被定义为

满足图 中存在大小为 的团，这是一个 问题，但是

满足 是 中顶点的一个子集且 是大小为 的团，这是一个 问题，其中 就扮演了 certificate 的角色

不是一个有实践意义的计算模型，因为现实生活中的计算不是非确定性的，但是 中语言的性质说明了这类问题的一个特征，即可以找到问题的一个实例并且可以有效地测试其是否是一个满足要求的解

如果定义

则各个 time complexity class 之间的关系为

而这些语言都是 decidable languages 的子集

Polynomial-Time Reductions

reduction 是一个 computable function ，而如果 是一个 poly-time computable function，则称这个 reduction 是 poly-time reduction，记为

poly-time computable: 对于函数 ，对于 ，存在一个 TM 满足对任意输入 ， 都会 halt 且在 tape 上留下

同样的，这个 reduction 隐含的意义为 至少和 一样难

则有，如果 ，则

Proof.

可以在 poly-time 将 的实例 转换为 的实例 ，且可以在 poly-time 使用 的 decider 判定 （由于 poly-time reduction，），由于多项式运算的封闭性，总体的时间仍是 poly-time 的

Q.E.D.

称一个语言 是 -complete ，如果其满足

如果仅满足第二条约束则称 是 -hard

证明一个语言 属于 可以分为两步

  1. 证明
  2. 对于已知的 ，有 （根据 poly-time reduction 的传递性可得其满足第二条约束）

对于 有如下结论

如果 且 ，则

Proof.

任取 ，有 ，而由于之前的结论，，则

Q.E.D.

SAT 指的是一个布尔表达式是否为 satisfiable 的问题，这个问题是一个 问题

一个布尔表达式是 satisfiable 的，说明存在一个对其中 variable 的 assignment 使得整个表达式为真

其证明的思路分为两部分

  • SAT 是 问题：只需要构造一个 NTM 猜测并验证 assignment
  • ：令 为判定 的 NTM，则对于输入 ，可以构造一个布尔表达式 ，满足 ，具体构造过程见课本 10.2.3 节

3SAT 是 SAT 问题的一个特例，即一个 3-cnf 的布尔表达式是否为 satisfiable

3SAT 也是 问题

图中的最大独立集（independent set, IS）：独立集 是一个点集，满足其中任意两点都没有边相连

图中的最大团（clique）：团 是一个点集满足其中任意两点都有边相连

图中的最小顶点覆盖（vertex cover, VC）：覆盖集 是一个点集，满足对任意边 ，其至少有一个顶点在 中

图中的 Hamilton 回路：存在一个环经过每个顶点且仅经过一次，类似的问题还有 TSP 问题

子集和问题（subset sum）：对于一个集合 存在一个子集 满足 中的数的和等于给定值