计算理论：Petri net 与 Timed Automata

course notes › theory of computation

Petri net and Timed Automata

Petri Net

automata 是一个理论的理想的模型

petri net 相对的更适合工程实现

  • state is distributed, transitions are localised
  • local causality replaces global time
  • subsystems interact by explicit communication

PN 中的状态迁移是异步的，因此可以用来建模并发分布式系统

Definition

PN 的图形化表示可以看作一个二分图（bipartite graph），顶点分为两类

  • places：用于建模系统中的资源或状态
  • transitions：用于建模系统中的状态迁移和同步

图中的边（arc）总是连接两种不同的顶点

Token 是位于 places 中的资源

更为正式的定义为

PN 是一个 4-tuple 其中

  • 是 places 的集合
  • 是 transitions 的集合
  • 是 transition 的输入，记为
  • 是 transition 的输出，记为

由于 token 的存在，故可以定义 marking 为各个 place 中 token 的数量

Basics of PN

Fire

对于一个 transition ， 在当前 marking 为 enabled 对于 的所有 input，其中都存在一个 token

一个 enabled transition 即可 fire ，即从其所有 input 中减去一个 token，再在其所有 output 中增加一个 token

Fire 是一个原子操作

PN 中的边可以带有权重，对于边带权的 PN，一个 transition 被 enabled 要求其所有 input 中的 token 数都大于等于对应边的权重

PN 可以为多种现实中的行为建模

  • 顺序执行：当前 transition 被 enabled 只能在前一个 transition fire 之后
  • 同步：所有 input 中都有 token（resource）后当前 transition 才能 fire
  • merge&fork：多个 resource 汇总到一个 place 或是 resource 从一个 place 分发到多个 place
  • 并发：多个 enabled transition 可以各自独立地 fire
  • conflict：多个 enabled transition 在其中一个 fire 之后其余便不处于 enable 状态

Run

PN 的 run 是一个有限/无限的 marking 和 transition 的序列

其中 是 PN 的初始 marking，而 ，且

上式的含义是从当前 marking 减去所有 的 input 再加上所有 的 output 即是 fire 之后的 marking

PN 的语义同样是基于 TS，其中状态为 marking，而 transition 即为 fire

Other definitions

  • source transition: no input
  • sink transition: no output
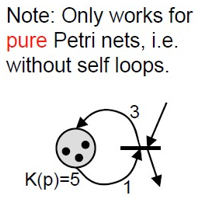
  • self-loop: a pair s. t.
  • pure PN: no self-loops
  • weighted PN: arcs with weight
  • ordinary PN: all arcs weights are 1
  • infinite capacity net: places can accommodate an unlimited number of tokens
  • finite capacity net: each place has a maximum capacity
  • strict transition rule: after firing, each output place can't have more than tokens

则有定理：任何 pure finite-capacity PN 可以被转换为等价的 infinite-capacity

具体做法为：

  • 对任意 ，添加一个 place ，其中初始 marking
  • 对任意 output arc ，添加 且权重为
  • 对任意 input arc ，添加 且权重为

如下图

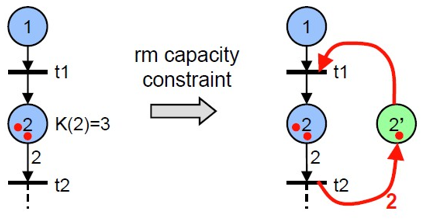
新添加的 满足了在 中的 token 数之和恒定且等于 ，但是对于有 self-loop 的便不能使用这种方法，如下图

在添加后变为了不能 fire 的状态

但是对于 non-pure 的 PN 可以通过消除 self-loop 的方式将其变为等价的 pure PN

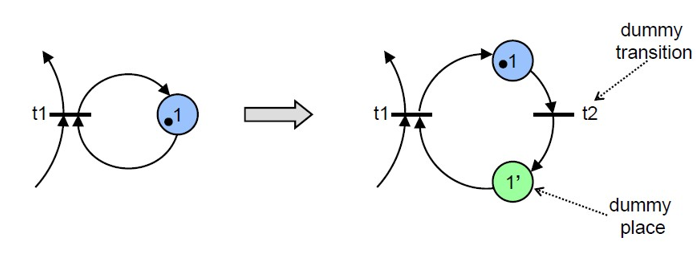
Behavioral properties

Behavioral peoperty 是取决于初始 marking 的属性

  • Reachability：称一个 marking 可达，如果存在一个从 到 的迁移序列
  • Boundness：一个 bounded PN 任意可达 marking 中 place 中的 token 不会超过某个上限。称 1-bounded 的 PN 为 safe PN
  • Liveness：即任何可达的 marking 都有 transition 可以 fire，等价于系统无死锁
  • Reversibility：任意可达的 marking 都可达初始 marking。对于 reversibility 有一个较为宽松的版本，即存在一个 home state 满足任意可达的 都可达
  • Persistence：对任意两个 enabled 的 transition，fire 其中一个不会导致另一个 disabled，即一个 transition 如果 enabled 则会一直持续到其 fire 为止
  • Fairness：每个 transition 连续 fire 的次数是有上限的

Cover tree

可以通过树的形式表现出所有可能的 marking

根节点为初始 marking，节点则是可达的 marking，通过 transition 的 fire 相连

对于 unboudned PN，引入 表示任意个数的 token，则有

  • PN 为 bounded 任何节点中不出现
  • PN safe 节点中只有 0，1
  • transition is dead 不出现在任何边中

在分析 PN 时代价往往是随着 PN 规模的增大指数级增长的，故需要化简 PN，常用的方法有

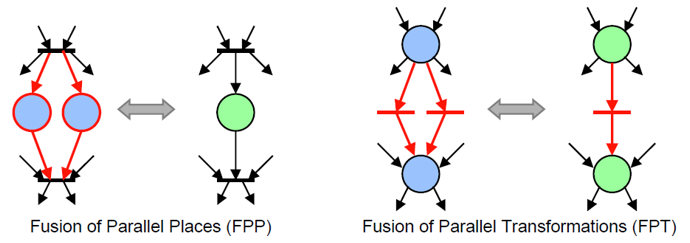
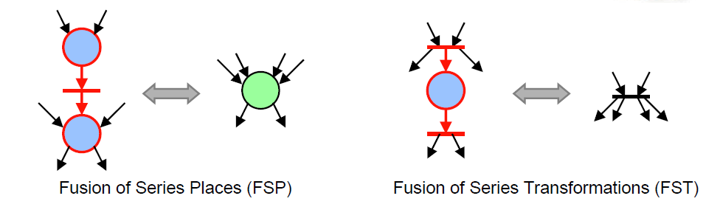
PN with time

Time PN 是在经典 PN 的基础上，为每个 transition 分配一个时间区间 ，其值与 最近一次 enabled 有关

如果 是在时间 enabled 的，则其能 fire 的时间一定位于 ，且 或是在 之前完成 fire 或是在 fire 之前因为另一个 transition 的 fire 而不再 enabled

fire 不需要花费时间

Time PN 的思路很符合常识：一个 Transition 在 enabled 之后不一定会立刻 fire，但一定会在某段时间过后 fire

time PN 的定义为

time PN 是一个 6-tuple ，其中

  • 是有限的 place 集合
  • 是有限的 transition 集合
  • 是 flow relation
  • 是 earliest fire time 和 latest fire time，满足
  • 是初始 marking

令 为非负实数（代表时间），则 中的状态是一个 pair ，其中 是 marking，且 被称为 clock function

对于初始状态 满足

则一个 transition 如果能在状态 以 的延迟 fire 等价于满足下列条件

在从 以延迟 fire 之后，新的状态 为

  • 对于任意 ，如果 则 ，否则

则 time PN 的 run 是一个 state，transition，delay 的序列

满足 是初始状态，且对任意 ，通过 transition 在 delay 后 fire 得到

time PN 可以为同步的 fire 添加时间上的先后关系

Timed Automata

TA 用于为实时系统建模，常见的有两种模型

Discrete Time Domain

基本思想是时钟每隔一个固定的时间间隔后发出信号，且系统在时钟发出信号后做出改变，在两次信号间的时候系统等待

选定一个基本的时间段 ，则任何事件发生的时间点只能是 的整数倍

挑战在于 的选取，常常用于建模同步系统，如硬件电路的建模

Continuous Time Domain

模型中时间以实数表示，而 delay 可以为任意小。这样建模的结果是状态空间往往是无限甚至不可数的，不能以遍历状态空间的方式解决问题

TA 是对于 FA 的扩展（添加了 clock），但是对于能对 clock 做的操作有限制

  • 能将 clock 的值与一个实数比较
  • 能将一个 clock reset 为 0
  • uniform flow of time：所有 clock 变化的速率是相同的

Definition

TA 的图形表示是一个二元图，节点为 location，边为 transition

  • 系统中有多个 clock，以相同速率运行
  • 时间只会在 location 消耗
  • 在边上有限制 clock 的 constraints，称为 guards。只有满足 guards 才能经由此边迁移到下一个 location
  • 在边上同样可以进行 clock 的 reset 操作
  • 在 location 上有限制 clock 的 invariants，只有满足 invariants 才能留在当前 location，否则必须进行 transition

Clock Constraints: 设 为 clock 的集合，则 为 clock constraints 的集合，其中的元素为

满足

则一个 TA 是一个 4-tuple ，其中

  • 是有限的 location 集合
  • 是有限的 clock 集合
  • 是初始的 location
  • 是边的集合，即边为一个 4-tuple (source location, clock constraints, set of clocks to be reset, target location)

Semantics

TA 的语义是基于 TS 的，其中

  • state 为 location + clock valuation
  • transition 可分为两种
    • wait，此时仅有 clock valuation 变化
    • action，location 的变化

clock valuation 是一个函数 ，代表当前的 clock 的值

  • 代表将 中的 clock 置为 0 后的 valuation，即

  • 代表 flow of time，即

  • 代表 满足 constraint

则可以给出 TA 语义的定义，TA 的语义是一个 TS

  • 是状态集合
  • 是初始状态
  • 是迁移
    • delay action:
    • discrete action: s. t.

上述定义未涵盖 invariants 的部分

invariants 可以看作一个从 location 到 constraint 的函数

Reachability Problem

TA 的某个 location 的可达性是一个 PSPACE-complete 的问题

其可判定性通过 region construction 得出，其基本思想为某些 clock valuation 是等价的，故可以将不可数的 clock valuation 划分为有限个等价类，基于等价类判断可达性

首先考虑 ，则可定义 为 的整数部分， 为 的小数部分

则两个 clock valuation 表示对于 TA 来说其不可区分（bisimulation）

令 为 constraints 中与 clock 所比较的常数中最大的一个，则 表示对所有 满足

  • 或是

则所有等价的 组成等价类 ，称为 region，其数量最多为