计算理论：迁移系统

course notes › theory of computation

Transition System

Definition

Transition System

TS 是一种 reactive system

It is used to describe the potential behavior of discrete systems. It consists of states and transitions between states, which may be labeled with labels chosen from a set; the same label may appear on more than one transition.

如果用图像来表示，TS 是一个二元图，node 代表 state，edge 代表 transition

更为正式的定义为

一个 TS 是一个 5-tuple ，其中

  • 是 state set（可以是无限甚至不可数的）
  • 是初始的状态
  • 是 transition set（可以是无限甚至不可数的）
  • 是两个从 到 的映射，对于 ， 代表其 source 和 target

如果 是 finite ，则称这个 TS 是 finite

Reachable and Terminal

如果一个 transition 的 source，target 分别是 ，则可以记为

根据此给出更为 general 的 transition

Basis. 如果 ，则有

Induction. 如果 ，则有

根据此即可定义一个状态的可达（reachable）

对于 TS ，如果对于 有 ，则称 reachable

而如果对于 ，不存在 满足 ，则称 为 terminal

若 为 terminal 且 reachable，则称 为 deadlock state

Path

一条长度为 的 path 是一个 transition 的序列 满足

上述定义是 finite path，而一个 infinite path 是一个 infinite 的 transition 序列 满足

若将所有 finite path 的集合记为 ，将所有 infinite path 的集合记为 ，则 可以扩展到

同样的， 可以扩展到

由此可以定义 上的 product，如果 是长度为 的 path，而 是长度为 的 path，且满足 ，则可定义

为长度为 的 path，且

product 也可推广到 ，定义与上述类似

Empty path：对于每个状态 ，都可以定义一条 empty path ，满足

则如果对于 path 有 ，则

Labeled transition system

A transition system labeled by an alphabet is a 6-tuple

其中

label 代表触发 的动作

一般来说不会有两个 transition 有相同的 source，target 以及 label，即 TS 中的 transition 都是可区分的（ 是单射），但是两个 transition 有相同的 source 和 target 是合理的

在 labeled TS 中，有 path ，则称 为 的迹（trace）

Equivalency for TS

等价关系是一种二元关系，满足自反，对称，传递。对于 TS 有很多种不同的等价定义方式

Homomorphism: 考虑两个 TS 与

从 到 的 homomorphism 是一对映射

满足

对于 labeled TS 还需满足

如果 都是 surjective，则称 homomorphism 是 surjective， 是 在 下的 quotient

strong isomorphism: 一个 TS strong isomorphism 是一个 TS homomorphism，满足 都是 bijective

显然如果 是 isomorphism 则 的逆也是一个 isomorphism

对于两个 strong isomorphic 的 TS，它们唯一的区别就是命名方式

weak isomorphism: 对于一个 TS ，其可达的状态集合定义为

则如果两个 TS 的 isomorphism 是定义在 上的，称这两个 TS weak isomorphism，即仅在可达的部分相同

显然，如果两个 TS isomorphic，则这两个 TS weak isomorphic

Bisimulation: 令 为两个 TS ，则 bisimulation 是一个二元关系 ，其定义为

Basis.

Induction.

  • 如果 且 ，则存在 满足 并且
  • 如果 且 ，则存在 满足 并且

这里的 transition 需要 label 相同（或是对应）

是 bisimulation equivalence 存在 bisimulation

两个 isomorphic 的 TS 一定是 bisimilar 的，但反之不真

Free Product of TS

考虑 个 TS

则其 free product 定义为

对于 labeled TS 同理

然而对于 product TS 来说，不是所有 transition 都是有意义的，因为要受到同步的限制

故有意义的 TS 是 free product 的一个子系统，其定义可表示为 synchronous product

如果 TS 对应的 label alphabet 为 ，且 是一个同步限制条件，则其 synchronous product 记为

是 free product 的子系统，仅包含满足 的 transition

在 free product 中，假设所有的 TS 都是同步执行的，但是有时候也需要体现出某个 TS 执行而其他 TS 没有执行的情况，故可以引入 -transition，即从任意状态 到其自身的 transition

在不同 TS 间有 shared label 的情况下 -transition 十分重要

Temporal Logic

Temporal Logic 用于形式化描述 reactive system 中 transition 的序列，而其中的属性可以用 CTL* 来描述

CTL* 可以用来描述 computation tree 的属性，computation tree 是从 TS 开始状态的所有可能执行路径

CTL* 的组成包括

  • path quantifier: A (for all computation path), E (for some computation path)
  • temporal: X, F, G, U, R
    • X (next time): the property holds in the second state of the path
    • F (eventually): the property will hold at some state on the path
    • G (always): the property holds at every state on the path
    • U (until): if there is a state on the path where the second property holds, at every preceding state, the first one holds
    • R (release): the second property holds along the path up to and include the first state where the first property holds. However, the first property is not required to hold eventually

一个例子如下

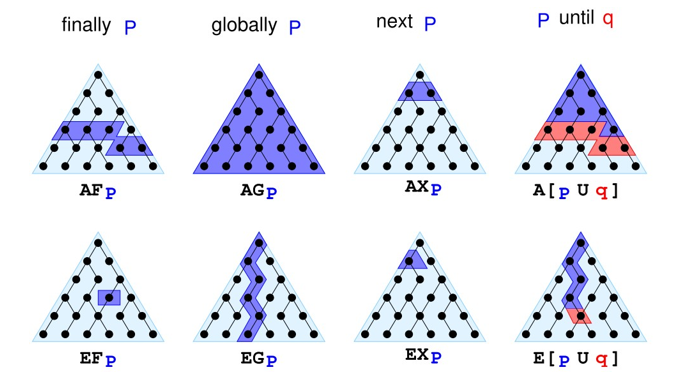
常见的用 CFL 描述的行为有

  • Safety: something bad will not happen，常用 AG 描述
  • Liveness: something good will happen，常用 AF 描述
  • Fairness: something is successful/allocated infinitely often，常用 AGAF 描述，即对于所有路径上的所有状态，都满足在之后的所有路径上都会在某个状态上满足条件